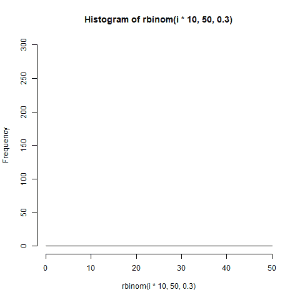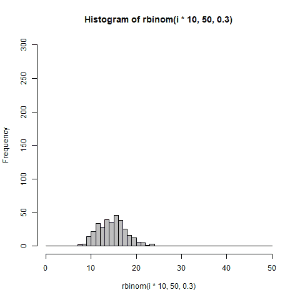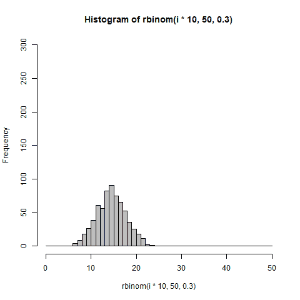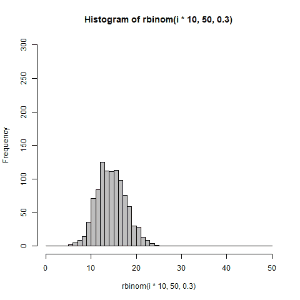
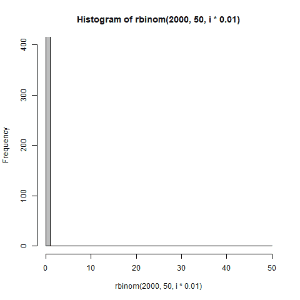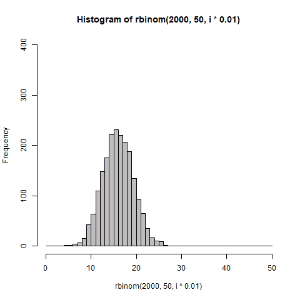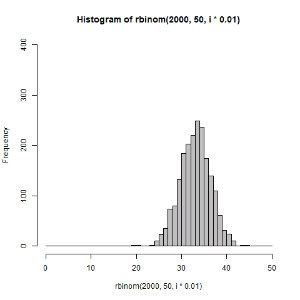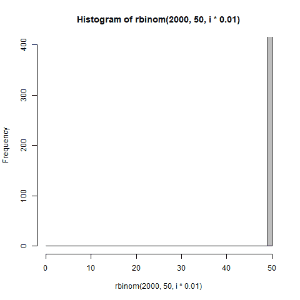
for文を使えるようになると,いろいろ便利です.以下のような図も作れます.
(左)二項分布 \(B(50,0.3)\) からのサンプリング数を1から1000まで変えてみた
(右)二項分布 \(B(50,p)\) のパラメータpを0~1の範囲で変えてサンプリングしてみた
◆準備
setwd()でワーキングディレクトリを指定し,演習用フォルダを指定しておいてください.参考:地理空間情報の可視化
◆二項分布に親しむ
表が出る確率がpのコインをn回投げて,表がk回出る確率の分布.
― 二項分布の数式 ―
問1 パラメータがそれぞれ \(n=50, p=0.3\) の 二項分布\(B(50,0.3)\) において,表が出る回数を \(k\) と表す.このとき, \(k=20\)となる確率を求めよ.
ヒント:dbinom(k,n,p)という関数を使うことで,\(B(n,p)\) において\(k\)が出る確率を求めることができる.
問2 パラメータがそれぞれ \(n=50, p=0.3\) の 二項分布\(B(50,0.3)\) から,20個の乱数をサンプリングせよ.
ヒント:rbinom(size,n,p)という関数を使うことで,\(B(n,p)\) からsize個の乱数をサンプリングすることが出来る.
◆for文を使ってみる!
for文は,以下のような構文である.Rのfor文では,()内のiに,vectorの値をひとつずつ入れて, {} 内の処理をおこなう.たとえば,for(i in 1:5)であれば,i=1, i=2, i=3, i=4, i=5をそれぞれ代入し,{}内のprint(i)を実行する.print関数は()内のオブジェクトをコンソールに吐き出す関数である.
printをしないでiだけ書くとどうなるかも試してみよう.
for (i in vector) {
print(i)
}
問3 \(n=50, p=0.3\) の 二項分布\(B(50,0.3)\) において、表が出る回数\( k \)が, \( 0,1,2,…50 \) となる確率をすべて計算せよ.
ヒント:もちろん,1行ずつkを変えて…となると大変.for文を使おう.????に繰り返したい値をベクトルに入れて,指定する.i,n,pもそれぞれ指定する.print関数をつけないとどうなるか…?
for (i in ????) {
dbinom(i,n,p)
}
問4 \(n=50, p=0.3\) の 二項分布\(B(50,0.3)\) から、20個の乱数をサンプリングする,という操作を100回繰り返し,その結果を表示せよ.
ヒント: ????に繰り返したい値をベクトルに入れて,指定する.i,n,pもそれぞれ指定する.print関数を使って表示する.
for (j in ????) {
rbinom(size,n,p)
}
◆for文を使って可視化する
for文を使うと,条件を少しずつ変えたグラフなども簡単に作れる.
問5 \(n=50, p=0.3\) の 二項分布\(B(50,0.3)\) において、表が出る回数\( k \)が, \( 0,1,2,…50 \) となる確率をすべて計算し,x軸にkを,y軸にkが出る確率をとった二次元のグラフを作成してみよう.
ヒント1:これもfor文を使うこと(for文を使わない方法もある).
ヒント2:グラフを出力する関数はplot()である.plot(x,y)で,横軸がx,縦軸がyのグラフが描かれる(xとyのベクトルの長さは同じでなければならない).
ヒント3:par(new=T)をplot関数の前に指定することで,その前に書いたグラフに重ね書きができる.
for (i in ????) {
plot(i,dbinom(i,n,p))
par(new=T)
}
ヒント4:x軸とy軸がぐちゃぐちゃになったのではないでしょうか?そういう時は,以下のようにxlim,ylim というパラメータを指定することで,毎回同じ範囲の軸を描くことが出来る.1回目だけ描いて2回目以降は描かないように指定することで,重ね書きによって文字が分厚くなることも防げそうだが,今回はそれはやらない.
xlim = c(0,50),ylim = c(0,0.2)
問6 \(n=50, p=0.3\) の 二項分布\(B(50,0.3)\) から、20個の乱数をサンプリングする,という操作を100回繰り返し,その結果をヒストグラムに書き表してみよう.
ヒント:breaksというパラメータを使って,ヒストグラムの範囲と幅を指定することが出来る.たとえば,以下のようにパラメータ指定すると,0から50の値を幅1で表示する,というものになる.
ヒント2:黒々として見にくければ,colというパラメータで色を分けて指定することもできる.col = i のように指定すれば,毎回色を変えて可視化することができる.
問7 \(n=50, p=0.3\) の 二項分布\(B(50,0.3)\) において、表が出る回数\( k \)が, \( 0,1,2,…50 \) となる確率を計算し,その確率に各々50をかけた値をy軸にして表示せよ.また,これを問6のグラフに重ね合わせてみよう.
◆ファイルの出力
問8 ファイルに出力する.
まずは,setwdで保存したいフォルダのパスを指定する.
setwd("保存したいフォルダのパス")
getwd()
ファイルに画像データを保存する場合は, plot()の前 にpng(“パス/ファイル名”)を実行し, plot()の実行後,dev.off()を実行することで,plot()で描いたグラフが “パス/ファイル名” に保存される.
ファイル名が同じだと,毎回上書きされてしまう.これでは困る.ファイル名を各繰り返しの度に変えたい.
そこで,paste()という関数を使う.これは,paste(“Hides”,”hima”)のように実行すると”Hideshima”のように,文字列をくっつけてくれる関数である.これを使って,毎回異なるファイル名を指定できるようにしてみよう.
sep = “” というパラメータをつけないと, “Hides hima” のようにスペースが入る.
paste("Hides","hima",sep = "")
実行後,指定したフォルダ内を確認してみよう.
for (i in 0:50) {
png(paste("binom",i,".png"))
hist(rbinom(20,50,0.3),xlim = c(0,50),ylim = c(0,20),breaks=seq(0,50,1),col = i)
dev.off()
}
◆動画の作成
「 png 複数 gif化 」等で各自ネットで調べてください.
◆演習の解答
以下は解答例です.もっといいやり方もあると思うので,各自模索してみてください.
下記コードのダウンロードはこちらから.
# 2020.6.3
# coded by F.Nakai
#二項分布
### 肩慣らし
#Q1: p=0.3, N=50の二項分布において、k=20となる確率
dbinom(20,50,0.3)
#Q2: p=0.3, N=50の二項分布から、20個の乱数をサンプリングする
rbinom(20,50,0.3)
### for文を使ってみる!
#Q3: p=0.3, N=50の二項分布において、K=0,1,2,...50となる確率を計算する
for (i in 0:50) {
print(dbinom(i,50,0.3))
}
#Q4:p=0.3, N=5の二項分布から、20個の乱数をサンプリングするのを100回繰り返す
for (j in 1:100) {
print(rbinom(20,50,0.3))
}
### for文を使って可視化してみる
#Q5: p=0.3, N=50の二項分布において、K=0,1,2,...50となる確率を計算して可視化する
for (i in 0:50) {
print(dbinom(i,50,0.3))
plot(i,dbinom(i,50,0.3),xlim = c(0,50),ylim = c(0,0.2))
par(new=T)
}
#Q6:p=0.3, N=50の二項分布から、20個の乱数をサンプリングするのを100回繰り返す
par(new=F)
for (j in 1:100) {
print(rbinom(20,50,0.3))
hist(rbinom(20,50,0.3),xlim = c(0,50),ylim = c(0,20),breaks=seq(0,50,1),col = j)
par(new=T)
}
#Q7: p=0.3, N=50の二項分布において、K=0,1,2,...50となる確率を計算し、回数に変換して可視化する
par(new=T)
for (i in 0:50) {
print(dbinom(i,50,0.3))
plot(i,dbinom(i,50,0.3)*50,xlim = c(0,50),ylim = c(0,20))
par(new=T)
}
#Q8: ファイルにつくったグラフを保存する.
#出力するフォルダを指定する.
setwd("保存したいフォルダのパスを設定")
getwd()
paste("hides","hima",sep = "")
#for文で1つずつグラフを書いていく
par(new=T)
for (i in 0:100) {
png(paste("binom",i,".png"))
hist(rbinom(i*10,50,0.3),xlim = c(0,50),ylim = c(0,300),breaks=seq(0,50,1),col = "gray")
dev.off()
}
#maptoolsライブラリを使ってみる
#グラフのプロットにラベルを付ける
library(maptools)
mes <- c("今","日","は","お","つ","か","れ","さ","ま","で","し","た","!")
mes1 <- length(rep(mes,5))
for (i in seq(1,50,1)) {
png(paste("binom",i,".png"))
plot(i,dbinom(i,50,0.3),xlim = c(0,50),ylim = c(0,0.2),col = "white",pch = 19,cex = 10)
pointLabel(x=i, y=dbinom(i,50,0.3), labels=mes[i])
dev.off()
}